Trigonometría para 1º Bachillerato

Como ya os dije, os dejo aquí los ejercicios del último examen (trigonometría) para que los que los que queráis podáis repasar el tema. Os recuerdo que la suma de los puntos es 9,5 porque hicimos una primera parte de fórmulas.
Buenas vacaciones para todos.

A partir de enero...

Carta de un profesor a sus alumnos suspensos. No tiene desperdicio, escuchadla:

Criterios de semejanza de triángulos

CRITERIO 1 DE SEMEJANZA DE TRIÁNGULOS


CRITERIO 2 DE SEMEJANZA DE TRIÁNGULOS

CRITERIO 3 DE SEMEJANZA DE TRIÁNGULOS

Animaciones de anomerico1

Complejos básicos

Como no podemos estar "sin complejos", nos quedaremos con los "complejos básicos".
Fuera de bromas, con esta animación podéis comprobar si vuestros cálculos de módulos y argumentos de complejos en forma binaria son correctos. Para acceder, pincha en la imagen:

Acertijo 1: Monstruos

Iniciamos hoy una sección de acertijos. Podéis poner vestras respuestas a través de los comentarios, que quedan pendientes de moderación.

Partiremos de una situación muy cotidiana: encerramos en una habitación a un monstruo que, cada día, duplica su volumen. Tarda 100 días en ocuparla completamente. 
¿Cuánto hubieran tardado si, en lugar de uno, encerramos a dos monstruos iguales?

NOTA: Aunque se puede resolver mediante una deducción lógica, Si tu respuesta tiene "armazón" matemático, indícalo en el comentario y muéstraselo en papel a la profesora. Recuerda que acabamos de ver las ecuaciones exponenciales... duplica su volumen... no digo más.

SOLUCIÓN

Los números complejos

Os dejo la presentación sobre los Números Complejos que estamos utilizando en la clase de 1º Bachillerato CyT. Hay alguna modificación respecto a la utilizada el día que comenzamos el tema. Creo que es la definitiva (nunca se sabe...)

¿Quién era Evariste Galois?

A pesar del tiempo que le estamos dedicando al ágebra en clase (polinomios, factorizaciones, ecuaciones de todo tipo, especialmente polinómicas...), seguramente no sabréis responder a la pregunta del título.
Os propongo desde aquí la lectura de un breve e interesante articulo que el matemático aragonés Fernando Corbalán publicó el pasado mes de octubre en el blog Café y Teoremas, en el que colabora, sobre este personaje clave en la historia del álgebra.  Se titula

"Galois, el matemático que se convirtió en genio antes de los 21 años"

El principio no puede ser más sugerente: "¿Cuántas personas conoces que habiendo vivido menos de 21 años hayan pasado a la historia?", pregunta Fernando. ¿Conoces a algún personaje que falleciera con esa edad y,  pesar de ello pasara a la historia por su aportación?
Esta va a ser una buena forma de comenzar el trabajo a realizar a partir de este artículo sobre Evariste Galois.

PROPUESTA DE TRABAJO
Cuestionario:
Antes de la lectura:

• D1.-  La primera es la pregunta de Fernando: ¿Cuántas personas conoces que habiendo vivido menos de 21 años hayan pasado a la historia? Indica quiénes y qué aportaron a la sociedad. Puede ser de cualquier disciplina, pero que realmente hayan hecho una aportación interesante en algún campo: ciencia, arte, cultura...
• D2.- Explica brevemente cómo resuleves tú las ecuaciones polinómicas de distintos grados. (No más de un par de líneas por grado) ¿Crees que así puedes resolver CUALQUIER ecuación polinómica de ese grado? En caso negativo, comenta qué tipos de soluciones no podrías encontrar. (La profesora lo ha comentado en clase en repetidas ocasiones)

Ahora lee atentamente el artículo.

Después de la lectura:

• D3.- ¿Quién era Evariste Galois? Anota brevemente los datos biográficos y explica cómo murió y a qué edad.
• D4.- En el artículo se habla de actividades de Evariste fuera de las matemáticas. Coméntalas.
• D5.- Siendo tan joven, su trabajo con las matemáticas fue enorme. Explica en qué consistió su aportación a la resolución de ecuaciones (polinómicas).
• D6.- En el texto se comenta el Teorema Fundamental de Álgebra. Enúncialo como lo hemos visto en clase y compáralo con el del texto. ¿Quién lo enunció y quién lo demostró? Busca los datos biográficos básicos de estos dos matemáticos (fechas y ciudad/país de nacimiento y muerte)
• D7.- El autor enmarca la vida de Evariste en "una época de grandes cambios (inicio de las máquinas de vapor y de los ferrocarriles, de la dinamo, del cloroformo y de la vacuna de la viruela, entre muchos otros), en la que se fraguó nuestro presente, y de ilustres personajes, como Verdi, Marx, Lord Byron, Champollion, Goya y Darwin." ¿De qué siglo hablamos? ¿Qué pasaba en España en aquella época? (quién gobernaba y reinaba, qué hechos destacados se produjeron...) 
• D8.- Haz una breve semblanza (de un par de líneas) de cada personaje nombrado en la cuestión anterior.
• D9.- Breve reseña del autor del artículo y del blog en el que se encuentra.

Formato del trabajo:

• El formato empleado será el de presentación de diapositivas.
• Cada cuestión debe quedar resuelta en una diapositiva, y a la lista anterior hay que añadir una "portada"
• Las preguntas NO deben aparecer en las diapositivas. Sólo las respuestas, bien redactadas.
• No abuses del texto: debe estar el justo, sin ser pesado. Procura repartirlo en varios cuadros de texto si lo permite la cuestión.
• Cada diapositiva deberá tener alguna ilustración y algún enlace de ampliación del contenido.

Evaluación:
Para calificar el trabajo, se tendrá en cuenta:
- Que estén respondidas todas las cuestiones
- La calidad de las respuestas
- Que el formato se ajuste a lo indicado en el punto anterior.

El trabajo supondrá un 4% de la nota dedicada a exámenes y trabajos (90%)
Fecha de entrega: miércoles 7 de diciembre. No lo dejes para el final. Si tienes alguna duda, pregúntale a la profesora,... pero con tiempo.

Raíces cuadradas con Mati

El algoritmo para resolver una raíz cuadrada es un verdadero engorro, difícil de recordar porque no resulta significativo.
En "Esas raíces tan... cuadradas", Clara Grima, a través de su personaje Mati, (de Mati y sus Matiaventuras) nos propone una alternativa mucho más razonable.

Propuesta de trabajo:
1.- Lee atentamente la lectura completa.
2.- ¿Qué personajes aparecen? Escribe los nombre y una breve descripción de quiénes son.
3.- ¿Quién neesita hacer raíces cuadradas y por qué?
4.- En la lectura se comienza calculando la raíz de cierto número por aproximación. ¿Qué número es? ¿Cuál es su raíz entera y su resto?
5.- ¿Cuál es la raíz entera y el resto de 153?
6.- Realiza una tabla similar a la de las imágenes del cuaderno para calcular la raíz del número 153 con tres cifras decimales (lee atentamente para ver cómo hacerlo).
7.- ¿Cuál es la raíz entera y el resto de 172?
8.- Realiza la misma tabla para aproximar con 3 cifras decimales el número 172.
9.- Lee atentamente de nuevo la parte correspondiente al algoritmo de resolución de caíces cuadradas. ¿Te parece más sencillo o más complicado? Es el que tienes en tu libro de texto. ¿En qué página está?
10.- ¿Por qué crees que han puesto la foto del final del artículo?

Nivel: 2º ESO
Fecha de entrega: 17 de noviembre de 2016

Concurso de microrelatos matemáticos

La Real Sociedad Matemática Española, el Instituto Universitario de Matemáticas y Aplicaciones y la Sociedad Aragonesa de Profesores de Matemáticas "Pedro Sánchez Ciruelo" han convocado un Concruso de Microrelatos Matemáticos dirigido a alumnado de Primaria, Secundaria Obligatoria, Formación Profesional Básica, Bachillerato o Ciclos Formativos de Grado Medio o Superior de los centros educativos de Aragón.

El concurso consiste en la redacción de un microrrelato matemático original. Los interesados presentarán un relato ideado por el autor en el que las matemáticas formen una parte importante en el desarrollo del mismo, bien a través de los personajes (ficticios o reales), de la trama (como por ejemplo, un mundo sin números) o de cualquier otra manera.

Los microrrelatos ganadores serán impresos para su difusión pública en los Autobuses Urbanos de Zaragoza del 24 de enero al 7 de febrero de 2017.

El plazo para enviar originales acaba el día 24 de noviemvre de 2016.

Consulta las bases aquí

Potencias de 10

Revisando la notación científica, hemos visto este vídeo que, aunque un poco viejo, nos muestra la enorme diferencia de cantidad que aparece al cambiar en una sola unidad el orden de magnitud, es decir, el exponente de la potencia de 10. Sobre todo si éstos son números altos.

Practica la estadística unidimensional

Haz el siguiente ejercicio en tu cuaderno y luego comprueba la solución.Si no puedes ver la solución bien, pincha el siguiente enlace: https://www.geogebra.org/m/h9xNAhyP



Autor de la escena: Joaquín Jiménez Ramos https://www.geogebra.org/joaquin.jimenez

Para practicar la fracción generatriz

En la siguiente animación puedes practicar el cálculo de la fracción generatriz. Oculta el resultado hasta que lo hayas completado.

Tipos de sistemas de ecuaciones lineales

 

Los Irracionales

Aunque pueda parecer el nombre de una peña, los Irracionales es un conjunto numérico que engloba aquellos números que tienen infinitos decimales no periódicos. Por ejemplo Pi, o raíz de dos.

¿Se puede afirmar que raíz de dos no tiene periodo en sus decimales, sin necesidad de calcularlos todos (o al menos muchos)? Sí. En este enlace tienes una demostración matemática de que raíz de dos es irracional.

Estos número dieron no pocos quebraderos de cabeza a los Pitagóricos, que creían (y deseaban) que todo el universo se podía explicar a partir de los números Racionales (cocientes de enteros). Pero descubrieron que existían los Irracionales (a los que llamaron Inconmensurables).

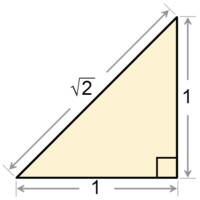
Teodoro de Cirene (465 a. C. - 398 a. C.), discípulo de Pitágoras, ideó una manera de representar segmentos cuya longitud es la raíz cuadrada de los número naturales, es decir, representó números irracionales. Al dibujarlos, los segmentos forman lo que llamamos la Espiral de Teodoro:

No es realmente una espiral porque no es una curva, pero se le parece. La figura está formada por una serie de triángulos rectángulos en los que un cateto mide 1u, el otro mide la raíz anterior y cuya hipotenusa es la nueva raíz.
Esta animación te muestra su construcción:


¿Te animas a dibujarla? Con un poco de imaginación se pueden decorar, como hicieron los alumnos del IES Salvador Victoria en estos trabajos (pincha sobre la imagen para verlos todos):

El curso pasado, con motivo del Día Internacional de las Matemáticas, los alumnos de 4ºESO trazaron una Espiral de Teodoro junto a la exposición "Nuestr@s Matemátic@s":

Por cierto, el artículo El infinito y más acá de Claudi Alsina, en el blog divulgativo El juego de la Ciencia del diario El País, ofrece una explicación clara y accesible de la demostración de que la raíz cuadrada de 2 no se puede poner como una fraccción. ¿Te atrves con ella?

La aguja de Buffon: Otra forma de calcular el número Pi

Mates y fotos: Funciones I

Mates y fotos: Funciones II

Sobre el número e

Programa de la serie "Mas por menos" sobre el número e

Concurso de Tamgram

El programa Conexión matemática pone en marcha un concurso para construir figuras con el Tangram, online.
Puedes acceder desde esta página. Tienes de tiempo para participar hasta el 14 de junio.
No olvides registrarte para relacionar tus datos con tu seudónimo.

Funciones II

Aquí queda la segunda entrega:

Parcelar usando el teorema de Pitágoras

En el patio del edificio nuevo del instituto se van a hacer parcelas para establecer distintos cultivos tradicionales.
Como se desea que sean parcelas rectangulares, necesitamos que las esquinas sean ángulos rectos.
Lo haremos con el método de los antiguos egipcios: con la terna pitagórica 3, 4, 5:

Para ampliar, ver este enlace.

Polígonos y poliedros con Troncho y Poncho

Áreas de polígonos:

Volúmenes y áreas de poliedros:

Parámetros de una parábola

Prueba a cambiar los valores de a, b y c y observa los cambio en la expresión algebraica de la parábla, y sobre todo, en la gráfica. Luego, responde en tu cuaderno a las siguientes preguntas:
- ¿Qué ocurre si c es muy grande? ¿Y si es negativa? ¿Por qué?
- ¿Qué ocurre si a es muy grande? ¿Y si es negativa?

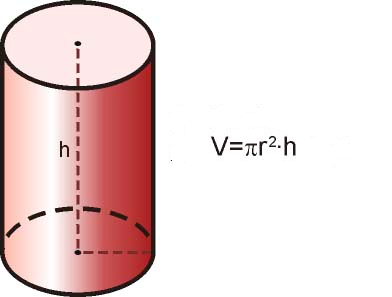
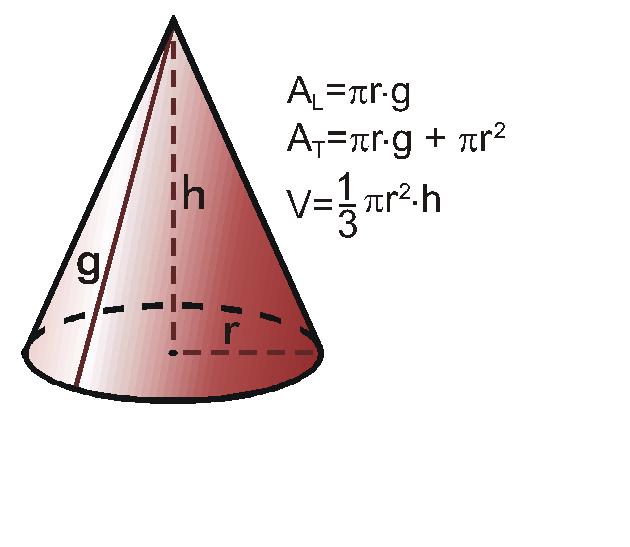
Volumen del cilindro y del cono

El volumen de un cono es un tercio del volumen del cilindro de la misma base y altura. Eso significa que necesitamos tres conos para "llenar" un cilindro:

Recuerda que:

  

Calculando Pi

Después de ver este vídeo del matemático Marcu Du Sautoy... ¿te animas a hacer tu propio cálculo del número Pi?

Mates y Fotos: Geometría II

Mates y Fotos: Geometría I

Funciones I

Os dejo la primera parte del tema Funciones, que estamos viendo en clase estos días en 4º ESO Op. B

Extraterrestres

El otro día en clase, no me explico muy bien cómo, nos encontramos preguntándonos si habrá vida inteligente en nuestro planeta...
En la web de Clara Grima Matiaventuras que os enlazo en la imagen nos habla de la ecuación de Drake que sirve para estimar el número de planetas que podrían albergarla... en nuestra galaxia.

¿Cuántas galaxias conocidas hay? Haz tus propios cálculos...

Proyecciones del mundo

En el blog Activate ya Blog nos cuentan algo sobre las diferentes visiones del mundo que ofrecen las distintas proyecciones de la "casi esfera" que es nuestro planeta, sobre el plano que nos ofrece un papel.
Representar de forma exacta una esfera sobre un plano es imposible. Por eso todo mapamundi es inexacto. La cuestión es cuál elegimos para representar nuestro planeta.

Podemos elegir entre proyecciones globulares, cenitales, o proyecciones cilíndricas como la de Mercator o Gall-Peters. ¿Cuál usar? Depende de la parte del mundo que queramos mostrar con mayor precisión.

Imagen tomada de Wikipedia

Para entenderlo mejor, podemos ver este artículo del blog Recuerdos de Pandora en el que se muestran las deformaciones de distintas proyecciones sobre el dibujo de una cabeza. 

Ejercicios de refuerzo de vectores, resueltos

Los ejercicios de Semana Santa son:
Hoja 1
Hoja 2

Aquí puedes descargar las resoluciones de las hojas de ejercicios de refuerzo para trabajar vectores y rectas (Para 4º ESO, Op B)

Hoja 1 "Ejercicios de vectores y rectas. Para Semana Santa"
Hoja 2 "Ejercicios de repaso de Geometría Analítica"

Solucionario de los ejercicios del libro

Ruffini... ¡en un rap!

Así es: el grupo italiano   os ofrece este rap con el método de división de polinomios entre binomios deltipo (x-a).
Recuerda que, para factorizar un polinomio (ponerlo como producto de otros del menor grado posible), buscamos un polinomio del tipo (x-a) tal que la división de nuestro polinomio entre él sea exacta, es decir, de resto cero. Para ello, buscamos el número a entre los divisores del término independiente, y efectuamos la división por el método de Ruffini. Aplicamos de nuevo el proceso al polinomio cociente de esa división.

Lo recordamos con un ejemplo:

Pero lo mejor es el rap que ha compuesto Lorenzo Baglioni Il trap del Teorema de Ruffini:

Ejercicios de 4º ESO

Para este fin de semana, debés realizar los siguientes ejerciciosdel tema de Geometría Analítica:
51, 52, 53, 54, 55, y  57
Me he enfrascado tanto e la explicación de clase que no me ha dado tiempo a decíroslo.
El aviso es para 4º A y para 4ºB
¡Buen finde!

Presentación de Geometría Analítica

Lo prometido es deuda. Aquí tenéis la presentación que hemos usado en clase completa. Repasad vuestros apuntes con ella:

Día de Pi

El día 14 de marzo se celebra el Día de Pi, ya que en el calendario anglosajón, el mes se nombra por delante del día, con lo que el 14 de marzo queda 3_14.
El año pasado (2015) fue un Día de Pi especial, ya que si añadimos a la fecha el año representado por lod dos últimos dígitos, nos quedaría esta espresión: 3_14_15 que es la parte entera y los cuatro primeros decimales de este famoso número.
Para celevrar este día, os dejo aquí una pequeña animación:

Teorema de Pitágoras

Primero experimentamos:

El Teorema de Pitágoras dice:

Al lado más largo se le llama hipotenusa y a los cortos, catetos. Por ello, el teorema se enuncia así:

En un triángulo rectángulo, el cuadrado de la hipotenusa es igual a la suma de los cuadrados de los catetos.

¡Ojo! Sólo sirve para triángulos rectángulos.

Ejemplo 1:

Demostración 1:

Demostración 2:

Suma de vectores

Actividad realizada por Antonio Monje

Historia de las Matemáticas

Conversión de medidas de ángulos con la calculadora

Os dejo este vídeo que nos muestra cómo convertir en una medida decimal un ángulo dado en grados, minutos y segundos:

Medición de alturas inaccesibles

Pincha en la imagen para acceder al formulario en el que hay que introducir los datos:

Áreas y volúmenes de cuerpos geométricos

A quien pueda interesar...

  

Demostración del Teorema del Coseno en clase

Y aquí tenemos la demostración del Teorema del Coseno:

Foto gentiliza de Maribel Mateo

Demostración del Teorema del Seno en clase

Aunque la imagen ha quedado un poco "chunga", aquí os dejo la demostración del Teorema del Seno realizada en clase.

Acertijos Matemáticos

Pincha en la imagen para descargar los acertijos de la Semana Matemática:

Refracción y Ley de Snell

Ya sabes que cuendo la luz atraviesa en agua, se desvía, produciendo el efecto óptico de que las cosas parece que están rotas.

Esto ocurre no sólo cuando la luz atraviesa el agua, sino en cualquier cambio de medio. Es debido a la diferencia de densidad.
¿Podremos calcular cuánto se desvía la luz?

Sí, el cálculo lo permite lo qe en óptica s llama la Ley de Snell de la refracción, que relaciona los ángulos de incidencia y refracción (a través del seno) con los índices de refracción de los dos medios (en este caso aire y agua):

En la siguiente imagen, extraída de esta página, se explica el fenómeno:

La pendiente en una carretera

Seguro que alguna vez has visto una señal de tráfico como la de la figura. Avisa de la pendiente del trazado de la carretera.
Ha dos formas de indicar esta pendinte: ambas usan las razones trigonométricas.

• Pendiente "matemática": es la tangente del ángulo. Por ejemplo, si se indica un 10% de pendiente, significa que por cada 100m recorridos en horizontal (cateto contiguo), se suben 10 en vertical (cateto opuesto). Por tanto, el ángulo que forma la carretera con la horizontal se puede calcular porque tiene 

tg x = 10/100

• Pendiente "de tráfico": en lugar de usar la tangente, usa el seno. Es decir, en este caso, una pendiente del 10% significa que por cada 100m recorridos sobre la carretera (hipotenusa) hemos subido 10m eb vertical (cateto opuesto). Por tanto, el ángulo que forma la carretera con la horizontal se puede calcular porque tiene 

sen x = 10/100

La imagen está extraída de este documento.

Razones trigonométricas de cualquier ángulo

Tales y la pirámide de Keops

Se cuenta que Tales de Mileto calculó la altura de la pirámide de Keops sin encaramarse a ella ni utilizar instrumento alguno de medida. Sólo aplicó la semejanza de triángulos.
Aquí tienes el método:

¿Qué medidas tuvo que tomar?

Procedencia de las imágenes y explicación completa en La Pirámide de Keops - Matemáticas cercanas

Semejanza. La presentación

Pincha sobre la imagen para descargar la presentación usada en el tema Semejanza.